约翰·冯·诺依曼
1903年12月28日
出生
1903年12月28日生于匈牙利布达佩斯的一个犹太人家庭。
1930年
撰写的《量子力学的数学基础》有极其重要的价值
1930年撰写的《量子力学的数学基础》已经被证明对原子物理学的发展有极其重要的价值。

1933年
解决希尔伯特第五问题
1933年运用紧致群解决了希尔伯特第五问题。
1936年 - 1943年
和默里创造了冯·诺伊曼代数
1936~1943年和默里合作,创造了算子环理论,即所谓的冯·诺伊曼代数。
1942年 - 1944年
凭借《博弈论和经济行为》成为数理经济学的奠基人之一
1942年起同莫根施特恩合作,写作《博弈论和经济行为》一书,这是博弈论(又称对策论)中的经典著作,使他成为数理经济学的奠基人之一。1944年发表了奠基性的重要论文《博弈论与经济行为》。论文中包含博弈论的纯粹数学形式的阐述以及对于实际博弈应用的详细说明。文中还包含了诸如统计理论等教学思想。

1944年
参加原子弹的研制工作
1944年参加原子弹的研制工作。
1945年3月
凭借“存储程序通用电子计算机方案”成为计算机之父
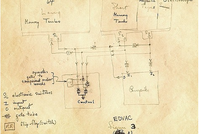
1945年3月他在共同讨论的基础上起草了一个全新的“存储程序通用电子计算机方案”--EDVAC(Electronic Discrete Variable Automatic Computer的缩写)。这对后来计算机的设计有决定性的影响,特别是确定计算机的结构,采用存储程序以及二进制编码等,至今仍为电子计算机设计者所遵循。这份报告是计算机发展史上一个划时代的文献,它向世界宣告:电子计算机的时代开始了。冯·诺依曼也因此被称为“计算机之父”。
1946年
开始研究程序编制问题,并取得很多成就
1946年开始研究程序编制问题,他是现代数值分析——计算数学的缔造者之一,他首先研究线性代数和算术的数值计算,后来着重研究非线性微分方程的离散化以及稳定问题,并给出误差的估计。他协助发展了一些算法,特别是蒙特卡罗方法。
1955年
被检查出患有癌症
1955年的夏天通过X射线检查出患有癌症。
1957年2月8日
在医院逝世,享年53岁
1957年2月8日在医院逝世,享年53岁。
冯·诺依曼,著名匈牙利裔美籍数学家、计算机科学家、物理学家和化学家。1903年12月28日生于匈牙利布达佩斯的一个犹太人家庭。

小时候的冯诺依曼
冯·诺依曼从小就显示出数学和记忆方面的天才,从孩提时代起,冯诺依曼就有过目不忘的天赋,六岁时他就能用希腊语同父亲互相开玩笑。六岁时他能心算做八位数除法,八岁时掌握微积分,在十岁时他花费了数月读完了一部四十八卷的世界史,并可以对当前发生的事件和历史上某个事件做出对比,并讨论两者的军事理论和政治策略,十二岁就读懂领会了波莱尔的大作《函数论》要义。

年轻时的冯·诺依曼
1914年夏天,约翰进入了大学预科班学习,是年7月28日,奥匈帝国借故向塞尔维亚宣战,揭开了第一次世界大战的序幕。由于战争动乱连年不断,冯·诺依曼全家离开过匈牙利,以后再重返布达佩斯。当然他的学业也会受到影响。但是在毕业考试时,冯·诺依曼的成绩仍名列前茅(除体育和书写外,都是A )。
1921年,冯·诺依曼通过“成熟”考试时,已被大家当作数学家了。他的第一篇论文是和菲克特合写的,那时他还不到18岁。麦克斯由于考虑到经济上原因,请人劝阻年方17的冯·诺依曼不要专攻数学,后来父子俩达成协议,冯·诺依曼便去攻读化学。
其后的四年间,冯·诺依曼在布达佩斯大学注册为数学方面的学生,但并不听课,只是每年按时参加考试,考试都得A 。与此同时,冯·诺依曼进入柏林大学(1921年),1923年又进入瑞士苏黎世联邦工业大学学习化学。1926年他在苏黎世联邦工业大学获得化学方面的大学毕业学位,通过在每学期期末回到布达佩斯大学通过课程考试,他也获得了布达佩斯大学数学博士学位。
冯·诺依曼的这种不参加听课只参加考试的求学方式,当时是非常特殊的,就整个欧洲来说也是完全不合规则的。但是这不合规则的学习方法,却又非常适合冯·诺依曼。
逗留在苏黎世期间,冯·诺依曼常常利用空余时间研读数学、写文章和数学家通信。在此期间冯·诺依曼受到了希尔伯特和他的学生施密特和外尔的思想影响,开始研究数理逻辑。当时外尔和波伊亚两位也在苏黎世,他和他们有过交往。一次外尔短期离开苏黎世,冯·诺依曼还代他上过课。聪慧加上得天独厚的栽培,冯·诺依曼在茁壮地成长,当他结束学生时代的时候,他已经漫步在数学、物理、化学三个领域的某些前沿。
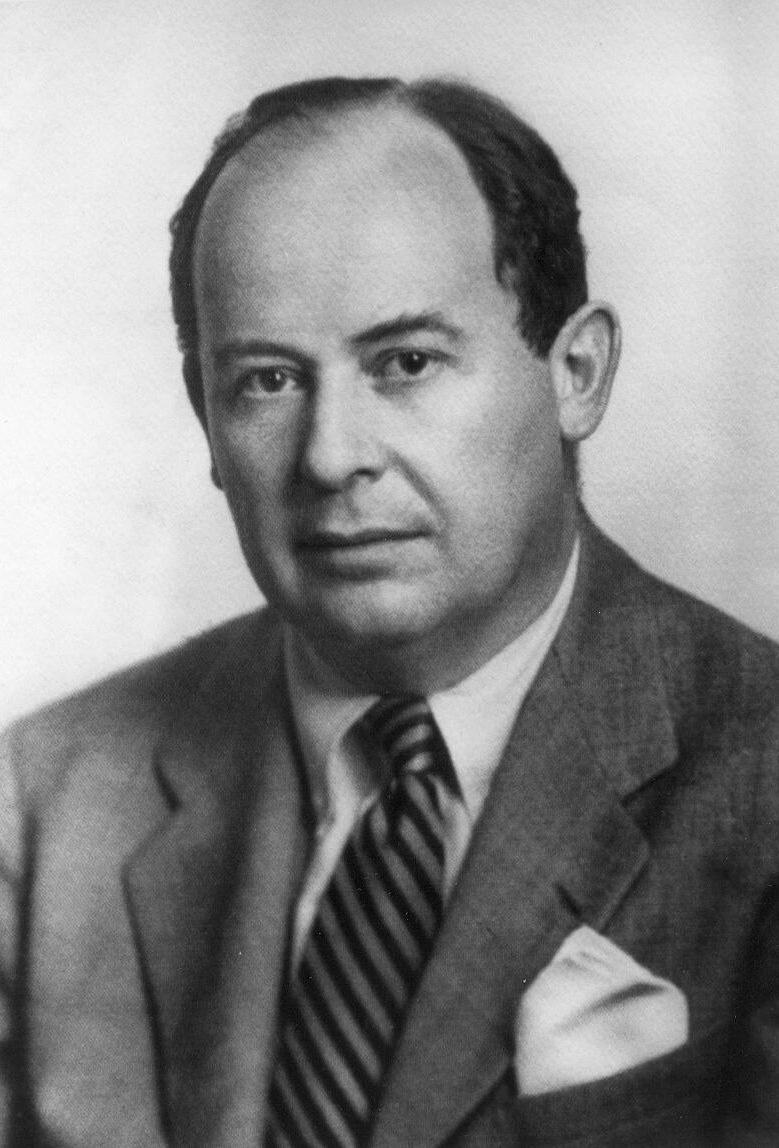
约翰·冯·诺依曼
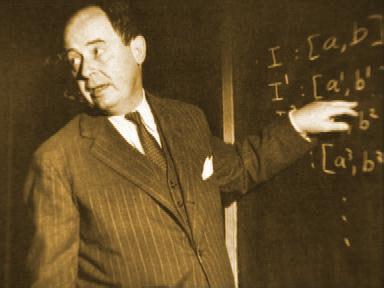
冯诺依曼在讲课(“用黑板擦证明定理”)
冯·诺依曼曾经算过,德国大学里现有的和可以期待的空缺很少,照他典型的推理得出,在三年内可以得到的教授任命数是三,而参加竞争的讲师则有40名之多。在普林斯顿,冯·诺依曼每到夏季就回欧洲,一直到1933年担任普林斯顿高级研究院教授为止。当时高级研究院聘有六名教授,其中就包括爱因斯坦,而年仅30岁的冯·诺依曼是他们当中最年轻的一位。
在高等研究院初创时间,欧洲来访者会发现,那里充满着一种极好的不拘礼节的、浓厚的研究风气。教授们的办公室设置在大学的“优美大厦”里,生活安定,思想活跃,高质量的研究成果层出不穷。可以这样说,那里集中了有史以来最多的有数学和物理头脑的人才。

冯诺依曼和妻子克拉拉
二次大战欧洲战事爆发后,冯·诺依曼的活动超越了普林斯顿,参与了同反法西斯战争有关的多项科学研究计划。1943年起他成了制造原子弹的顾问,战后仍在政府诸多部门和委员会中任职。1954年又成为美国原子能委员会成员。
冯·诺依曼的多年老友,原子能委员会主席斯特劳斯曾对他作过这样的评价:从他被任命到1955年深秋,冯·诺依曼干得很漂亮。他有一种使人望尘莫及的能力,最困难的问题到他手里。都会被分解成一件件看起来十分简单的事情,用这种办法,他大大地促进了原子能委员会的工作。
冯·诺依曼的健康状况一直很好,可是由于工作繁忙,到1954年他开始感到十分疲劳。

艾森豪威尔为冯·诺依曼颁奖
冯·诺伊曼是二十世纪最重要的数学家之一,在纯粹数学和应用数学方面都有杰出的贡献。他的工作大致可以分为两个时期:1940年以前,主要是纯粹数学的研究:在数理逻辑方面提出简单而明确的序数理论,并对集合论进行新的公理化,其中明确区别集合与类;其后,他研究希尔伯特空间上线性自伴算子谱理论,从而为量子力学打下数学基础;1930年起,他证明平均遍历定理开拓了遍历理论的新领域;1933年,他运用紧致群解决了希尔伯特第五问题;此外,他还在测度论、格论和连续几何学方面也有开创性的贡献;从1936~1943年,他和默里合作,创造了算子环理论,即所谓的冯·诺伊曼代数。

约翰·冯·诺依曼
冯·诺伊曼对世界上第一台电子计算机ENIAC(电子数字积分计算机)的设计提出过建议,1945年3月他在共同讨论的基础上起草了一个全新的“存储程序通用电子计算机方案”--EDVAC(Electronic Discrete Variable Automatic Computer的缩写)。这对后来计算机的设计有决定性的影响,特别是确定计算机的结构,采用存储程序以及二进制编码等,至今仍为电子计算机设计者所遵循。
1946年,冯·诺依曼开始研究程序编制问题,他是现代数值分析——计算数学的缔造者之一,他首先研究线性代数和算术的数值计算,后来着重研究非线性微分方程的离散化以及稳定问题,并给出误差的估计。他协助发展了一些算法,特别是蒙特卡罗方法。
40年代末,他开始研究自动机理论,研究一般逻辑理论以及自复制系统。在生命的最后时刻他深入比较天然自动机与人工自动机。他逝世后其未完成的手稿在1958年以《计算机与人脑》为名出版。
冯·诺伊曼的主要著作收集在《冯·诺伊曼全集》(6卷,1961)中。
无论在纯粹数学还是在应用数学研究方面,冯·诺依曼都显示了卓越的才能,取得了众多影响深远的重大成果。不断变换研究主题,常常在几种学科交叉渗透中获得成就是他的特色。
简单来说他的精髓贡献是两点:2进制思想与程序内存思想。

冯·诺依曼(右)等在世界上第一台计算机前
冯·诺依曼在数学的诸多领域都进行了开创性工作,并作出了重大贡献。在第二次世界大战前,他主要从事算子理论、集合论等方面的研究。1923年关于集合论中超限序数的论文,显示了冯·诺依曼处理集合论问题所特有的方式和风格。他把集会论加以公理化,他的公理化体系奠定了公理集合论的基础。他从公理出发,用代数方法导出了集合论中许多重要概念、基本运算、重要定理等。特别在1925年的一篇论文中,冯·诺依曼就指出了任何一种公理化系统中都存在着无法判定的命题。
1933年,冯·诺依曼解决了希尔伯特第5问题,即证明了局部欧几里得紧群是李群。1934年他又把紧群理论与波尔的殆周期函数理论统一起来。他还对一般拓扑群的结构有深刻的认识,弄清了它的代数结构和拓扑结构与实数是一致的。他对算子代数进行了开创性工作,并奠定了它的理论基础,从而建立了算子代数这门新的数学分支。这个分支在当代的有关数学文献中均称为冯·诺依曼代数。这是有限维空间中矩阵代数的自然推广。冯·诺依曼还创立了博弈论这一现代数学的又一重要分支。1944年发表了奠基性的重要论文《博弈论与经济行为》。论文中包含博弈论的纯粹数学形式的阐述以及对于实际博弈应用的详细说明。文中还包含了诸如统计理论等教学思想。冯·诺依曼在格论、连续几何、理论物理、动力学、连续介质力学、气象计算、原子能和经济学等领域都作过重要的工作。
冯·诺依曼对人类的最大贡献是对计算机科学、计算机技术、数值分析和经济学中的博弈论的开拓性工作。
一般认为ENIAC机是世界第一台电子计算机,它是由美国科学家研制的,于1946年2月14日在费城开始运行。其实由汤米、费劳尔斯等英国科学家研制的“科洛萨斯”计算机比ENIAC机问世早两年多,于1944年1月10日在布莱奇利园区开始运行。ENIAC机证明电子真空技术可以大大地提高计算技术,不过,ENIAC机本身存在两大缺点:(1)没有存储器;(2)它用布线接板进行控制,甚至要搭接几天,计算速度也就被这一工作抵消了。ENIAC机研制组的莫克利和埃克特显然是感到了这一点,他们也想尽快着手研制另一台计算机,以便改进。
1944年,诺伊曼参加原子弹的研制工作,该工作涉及到极为困难的计算。在对原子核反应过程的研究中,要对一个反应的传播做出“是”或“否”的回答。解决这一问题通常需要通过几十亿次的数学运算和逻辑指令,尽管最终的数据并不要求十分精确,但所有的中间运算过程均不可缺少,且要尽可能保持准确。他所在的洛·斯阿拉莫斯实验室为此聘用了一百多名女计算员,利用台式计算机从早到晚计算,还是远远不能满足需要。无穷无尽的数字和逻辑指令如同沙漠一样把人的智慧和精力吸尽。
被计算机所困扰的诺伊曼在一次极为偶然的机会中知道了ENIAC计算机的研制计划,从此他投身到计算机研制这一宏伟的事业中,建立了一生中最大的丰功伟绩。
1944年夏的一天,正在火车站候车的诺伊曼巧遇戈尔斯坦,并同他进行了短暂的交谈。当时,戈尔斯坦是美国弹道实验室的军方负责人,他正参与ENIAC计算机的研制工作。在交谈中,戈尔斯坦告诉了诺伊曼有关ENIAC的研制情况。具有远见卓识的诺伊曼为这一研制计划所吸引,他意识到了这项工作的深远意义。
冯·诺依曼由ENIAC机研制组的戈尔德斯廷中尉介绍参加ENIAC机研制小组后,便带领这批富有创新精神的年轻科技人员,向着更高的目标进军。1945年,他们在共同讨论的基础上,发表了一个全新的“存储程序通用电子计算机方案”--EDVAC(Electronic Discrete Variable Automatic Computer的缩写)。在这过程中,冯·诺依曼显示出他雄厚的数理基础知识,充分发挥了他的顾问作用及探索问题和综合分析的能力。诺伊曼以“关于EDVAC的报告草案”为题,起草了长达101页的总结报告。报告广泛而具体地介绍了制造电子计算机和程序设计的新思想。这份报告是计算机发展史上一个划时代的文献,它向世界宣告:电子计算机的时代开始了。
EDVAC方案明确奠定了新机器由五个部分组成,包括:运算器、控制器、存储器、输入和输出设备,并描述了这五部分的职能和相互关系。报告中,诺伊曼对EDVAC中的两大设计思想作了进一步的论证,为计算机的设计树立了一座里程碑。
设计思想之一是二进制,他根据电子元件双稳工作的特点,建议在电子计算机中采用二进制。报告提到了二进制的优点,并预言,二进制的采用将大简化机器的逻辑线路。
计算机基本工作原理是存储程序和程序控制,它是由世界著名数学家冯·诺依曼提出的。美籍匈牙利数学家冯·诺依曼被称为“计算机之父”。
实践证明了诺伊曼预言的正确性。如今,逻辑代数的应用已成为设计电子计算机的重要手段,在EDVAC中采用的主要逻辑线路也一直沿用着,只是对实现逻辑线路的工程方法和逻辑电路的分析方法作了改进。
冯诺依曼体系结构
说到计算机的发展,就不能不提到美国科学家冯诺依曼。从20世纪初,物理学和电子学科学家们就在争论制造可以进行数值计算的机器应该采用什么样的结构。人们被十进制这个人类习惯的计数方法所困扰。所以,那时以研制模拟计算机的呼声更为响亮和有力。20世纪30年代中期,美国科学家冯诺依曼大胆的提出,抛弃十进制,采用二进制作为数字计算机的数制基础。同时,他还说预先编制计算程序,然后由计算机来按照人们事前制定的计算顺序来执行数值计算工作。
冯诺依曼理论的要点是:数字计算机的数制采用二进制;计算机应该按照程序顺序执行。
人们把冯诺依曼的这个理论称为冯诺依曼体系结构。从ENIAC(ENIAC并不是冯诺依曼体系)到当前最先进的计算机都采用的是冯诺依曼体系结构。所以冯诺依曼是当之无愧的数字计算机之父。
根据冯诺依曼体系结构构成的计算机,必须具有如下功能:
把需要的程序和数据送至计算机中。
必须具有长期记忆程序、数据、中间结果及最终运算结果的能力。
能够完成各种算术、逻辑运算和数据传送等数据加工处理的能力。
能够根据需要控制程序走向,并能根据指令控制机器的各部件协调操作。
能够按照要求将处理结果输出给用户。
为了完成上述的功能,计算机必须具备五大基本组成部件,包括:
输入数据和程序的输入设备
记忆程序和数据的存储器
完成数据加工处理的运算器
控制程序执行的控制器
输出处理结果的输出设备
理论基础
冯·诺依曼的第一篇论文是和菲克特合写的,是关于车比雪夫多项式求根法的菲叶定理推广,注明的日期是1922年,那时冯·诺依曼还不满18岁。另一篇文章讨论一致稠密数列,用匈牙利文写就,题目的选取和证明手法的简洁显露出冯·诺依曼在代数技巧和集合论直观结合的特征。
1923年当冯·诺依曼还是苏黎世的大学生时,发表了超限序数的论文。文章第一句话就直率地声称“本文的目的是将康托的序数概念具体化、精确化”。他的关于序数的定义,已被普遍采用。
强烈企求探讨公理化是冯·诺依曼的愿望,大约从l925年到l929年,他的大多数文章都尝试着贯彻这种公理化精神,以至在理论物理研究中也如此。当时,他对集合论的表述处理,尤感不够形式化,在他1925年关于集合论公理系统的博士论文中,开始就说“本文的目的,是要给集合论以逻辑上无可非议的公理化论述”。
有趣的是,冯·诺依曼在论文中预感到任何一种形式的公理系统所具有的局限性,模糊地使人联想到后来由哥德尔证明的不完全性定理。对此文章,著名逻辑学家、公理集合论奠基人之一的弗兰克尔教授曾作过如下评价:“我不能坚持说我已把(文章的)一切理解了,但可以确有把握地说这是一件杰出的工作,并且透过他可以看到一位巨人”。
1928年冯·诺依曼发表了论文《集合论的公理化》,是对上述集合论的公理化处理。该系统十分简洁,它用第一型对象和第二型对象相应表示朴素集合论中的集合和集合的性质,用了一页多一点的纸就写好了系统的公理,它已足够建立朴素集合论的所有内容,并借此确立整个现代数学。
冯·诺依曼的系统给出了集合论的也许是第一个基础,所用的有限条公理,具有像初等几何那样简单的逻辑结构。冯·诺依曼从公理出发,巧妙地使用代数方法导出集合论中许多重要概念的能力简直叫人惊叹不已,所有这些也为他未来把兴趣落脚在计算机和“机械化”证明方面准备了条件。
20年代后期,冯·诺依曼参与了希尔伯特的元数学计划,发表过几篇证明部分算术公理无矛盾性的论文。l927年的论文《关于希尔伯特证明论》最为引人注目,它的主题是讨论如何把数学从矛盾中解脱出来。文章强调由希尔伯特等提出和发展的这个问题十分复杂,当时还未得到满意的解答。它还指出阿克曼排除矛盾的证明并不能在古典分析中实现。为此,冯·诺依曼对某个子系统作了严格的有限性证明。这离希尔伯特企求的最终解答似乎不远了。恰在此时,1930年哥德尔证明了不完全性定理。定理断言:在包含初等算术(或集合论)的无矛盾的形式系统中,系统的无矛盾性在系统内是不可证明的。至此,冯·诺依曼只能中止这方面的研究。
冯·诺依曼还得到过有关集合论本身的专门结果。他在数学基础和集合论方面的兴趣一直延续到他生命的结束。
纯粹数学
在1930~1940年间,冯·诺依曼在纯粹数学方面取得的成就更为集中,创作更趋于成熟,声誉也更高涨。后来在一张为国家科学院填的问答表中,冯·诺依曼选择了量子理论的数学基础、算子环理论、各态遍历定理三项作为他最重要数学工作。
1927年冯·诺依曼已经在量子力学领域内从事研究工作。他和希尔伯特以及诺戴姆联名发表了论文《量子力学基础》。该文的基础是希尔伯特1926年冬所作的关于量子力学新发展的讲演,诺戴姆帮助准备了讲演,冯·诺依曼则从事于该主题的数学形式化方面的工作。文章的目的是将经典力学中的精确函数关系用概率关系代替之。希尔伯特的元数学、公理化的方案在这个生气勃勃的领域里获得了施展,并且获得了理论物理和对应的数学体系间的同构关系。对这篇文章的历史重要性和影响无论如何评价都不会过高。冯·诺依曼在文章中还讨论了物理学中可观察算符的运算的轮廓和埃尔米特算子的性质,无疑,这些内容构成了《量子力学的数学基础》一书的序曲。
1932世界闻名的斯普林格出版社出版了他的《量子力学的数学基础》,它是冯·诺依曼主要著作之一,初版为德文,1943年出了法文版,1949年为西班牙文版,1955年被译成英文出版,至今仍不失为这方面的经典著作。当然他还在量子统计学、量子热力学、引力场等方面做了不少重要工作。
客观地说,在量子力学发展史上,冯·诺依曼至少作出过两个重要贡献:狄拉克对量子理论的数学处理在某种意义下是不够严格的,冯·诺依曼通过对无界算子的研究,发展了希尔伯特算子理论,弥补了这个不足;此外,冯·诺依曼明确指出,量子理论的统计特征并非由于从事测量的观察者之状态未知所致。借助于希尔伯特空间算子理论,他证明凡包括一般物理量缔合性的量子理论之假设,都必然引起这种结果。
对于冯·诺依曼的贡献,诺贝尔物理学奖获得者威格纳曾作过如下评价:“在量子力学方面的贡献,就是以确保他在当代物理学领域中的特殊地位。”
在冯·诺依曼的工作中,希尔伯特空间上的算子谱论和算子环论占有重要的支配地位,这方面的文章大约占了他发表的论文的三分之一。它们包括对线性算子性质的极为详细地分析,和对无限维空间中算子环进行代数方面的研究。
算子环理论始于1930年下半年,冯·诺依曼十分熟悉诺特和阿丁的非交换代数,很快就把它用于希尔伯特空间上有界线性算子组成的代数上去,后人把它称之为冯·诺依曼算子代数。
1936~1940年间,冯·诺依曼发表了六篇关于非交换算子环论文,可谓20世纪分析学方面的杰作,其影响一直延伸至今。冯·诺依曼曾在《量子力学的数学基础》中说过:由希尔伯特最早提出的思想就能够为物理学的量子论提供一个适当的基础,而不需再为这些物理理论引进新的数学构思。他在算子环方面的研究成果应验了这个目标。冯·诺依曼对这个课题的兴趣贯穿了他的整个生涯。
算子环理论的一个惊人的生长点是由冯·诺依曼命名的连续几何。普通几何学的维数为整数1、2、3等,冯·诺依曼在著作中已看到,决定一个空间的维数结构的,实际上是它所容许的旋转群。因而维数可以不再是整数,连续级数空间的几何学终于提出来了。
1932年,冯·诺依曼发表了关于遍历理论的论文,解决了遍历定理的证明,并用算子理论加以表述,它是在统计力学中遍历假设的严格处理的整个研究领域中,获得的第一项精确的数学结果。冯·诺依曼的这一成就,可能得再次归功于他所娴熟掌握的受到集合论影响的数学分析方法,和他自己在希尔伯特算子研究中创造的那些方法。它是20世纪数学分析研究领域中取得的最有影响成就之一,也标志着一个数学物理领域开始接近精确的现代分析的一般研究。
此外冯·诺依曼在实变函数论、测度论、拓扑、连续群、格论等数学领域也取得不少成果。1900年希尔伯特在那次著名的演说中,为20世纪数学研究提出了23个问题,冯·诺依曼也曾为解决希尔伯特第五问题作了决定性贡献。
应用数学
1940年,是冯·诺依曼科学生涯的一个转换点。在此之前,他是一位通晓物理学的登峰造极的纯粹数学家;此后则成了一位牢固掌握纯粹数学的出神入化的应用数学家。他开始关注当时把数学应用于物理领域去的最主要工具——偏微分方程。研究同时他还不断创新,把非古典数学应用到两个新领域:对策论和电子计算机。
冯·诺依曼的这个转变一方面来自他长期对数学物理问题的钟情;另一方面来自当时社会方面的需要。第二次世界大战爆发后,冯·诺依曼应召参与了许多军事科学研究计划和工程项目。1940~1957年任马里兰阿伯丁试验弹道研究实验室科学顾问;1941~1955年在华盛顿海军军械局;1943~1955年任洛斯·阿拉莫斯实验室顾问;1950~1955年,陆军特种武器设计委员会委员;1951~1957年。美国空军华盛顿科学顾问委员会成员;1953~1957年,原子能技术顾问小组成员;1954~1957年,导弹顾问委员会主席。
冯·诺依曼研究过连续介质力学。很久以来,他对湍流现象一直感兴趣。l937年他关注纳维—斯克克斯方程的统计处理可能性的讨论,1949年他为海军研究部写了《湍流的最新理论》。
冯·诺依曼研究过激波问题。他在这个领域中的大部分工作,直接来自国防需要。他在碰撞激波的相互作用方面贡献引人注目,其中有一结果,是首先严格证明了恰普曼—儒格假设,该假设与激波所引起的燃烧有关。关于激波反射理论的系统研究由他的《激波理论进展报告》开始。
冯·诺依曼研究过气象学。有相当一段时间,地球大气运动的流体力学方程组所提出的极为困难的问题一直吸引着他。随着电子计算机的出现,有可能对此问题作数值研究分析。冯·诺依曼搞出的第一个高度规模化的计算,处理的是一个二维模型,与地转近似有关。他相信人们最终能够了解、计算并实现控制以致改变气候。
冯·诺依曼还曾提出用聚变引爆核燃料的建议,并支持发展氢弹。1947年军队发嘉奖令,表扬他是物理学家、工程师、武器设计师和爱国主义者。
博弈论

冯诺依曼和摩根斯特恩
博弈论的一些想法,20年代初就曾有过,真正的创立还得从冯·诺依曼1928年关于社会博弈理论的论文算起。在这篇文章中,他证明了最小最大定理,这个定理用于处理一类最基本的二人对策问题。如果对策双方中的任何一方,对每种可能的策略,考虑了可能遭到的最大损失,从而选择“最大损失”最小的一种为“最优”策略,那么从统计角度来看,他就能够确保方案是最佳的。这方面的工作大致已达到完善。在同一篇论文中,冯·诺依曼也明确表述了n个游戏者之间的一般对策。
博弈论也被用于经济学。经济理论中的数学研究方法,大致可分为定性研究为目标的纯粹理论和以实证的、统计的研究为目标的计量经济学。前者称为数理经济学,正式确立于20世纪40年代之后。无论在思想上或方法上,都明显地受到对策论的影响。
数理经济学,过去模仿经典数学物理的技巧,所用的数学工具主要是微积分和微分方程、将经济问题当成经典力学问题处理。显然,几十个商人参加的贸易洽谈会,用经典数学分析处理,其复杂程度远远超过太阳系行星的运动,这种方法的效果往往很难是预期的。冯·诺依曼毅然放弃这种简单的机械类比,代之以新颖的博弈论观点和新的数学—和凸性的思想。
1944年,冯·诺依曼和摩根斯特恩合著的《博弈论和经济行为》是这方面的奠基性著作。将二人博弈推广到n人博弈结构并将博弈论系统的应用于经济领域,从而奠定了这一学科的基础和理论体系。论文包含了博弈论的纯粹数学形式的阐述以及对于实际应用的详细说明。这篇论文以及所作的与某些经济理论的基本问题的讨论,引起了对经济行为和某些社会学问题的各种不同研究,时至今日,这已是应用广泛、羽毛日益丰盛的一门数学学科。有些科学家热情颂扬它可能是“20世纪前半期最伟大的科学贡献之一”。
计算机
对冯·诺依曼声望有所贡献的最后一个课题是电子计算机和自动化理论。
早在洛斯阿拉莫斯,冯·诺依曼就明显看到,即使对一些理论物理的研究,只是为了得到定性的结果,单靠解析研究也已显得不够,必须辅之以数值计算。进行手工计算或使用台式计算机所需花费的时间是令人难以容忍的,于是冯·诺依曼劲头十足的开始从事电子计算机和计算方法的研究。
1944~1945年间,冯·诺依曼形成了现今所用的将一组数学过程转变为计算机指令语言的基本方法,当时的电子计算机(如ENIAC)缺少灵活性、普适性。冯·诺依曼关于机器中的固定的、普适线路系统,关于“流图”概念,关于“代码”概念为克服以上缺点作出了重大贡献。尽管对数理逻辑学家来说,这种安排是显见的。
计算机工程的发展也应大大归功于冯·诺依曼。计算机的逻辑图式,现代计算机中存储、速度、基本指令的选取以及线路之间相互作用的设计,都深深受到冯·诺依曼思想的影响。他不仅参与了电子管元件的计算机ENIAC的研制,并且还在普林斯顿高等研究院亲自督造了一台计算机。稍前,冯·诺依曼还和摩尔小组一起,写出了一个全新的存贮程序通用电子计算机方案EDVAC,长达101页的报告轰动了数学界。这一向专搞理论研究的普林斯顿高等研究院也批准让冯·诺依曼建造计算机,其依据就是这份报告。
速度超过人工计算千万倍的电子计算机,不仅极大地推动数值分析的进展,而且还在数学分析本身的基本方面,刺激着崭新的方法的出现。其中,由冯·诺依曼等制订的使用随机数处理确定性数学问题的蒙特卡洛法的蓬勃发展,就是突出的实例。
19世纪那种数学物理原理的精确的数学表述,在现代物理中似乎十分缺乏。基本粒子研究中出现的纷繁复杂的结构,令人眼花缭乱,要想很快找到数学综合理论希望还很渺茫。单从综合角度看,且不提在处理某些偏微分方程时所遇到的分析困难,要想获得精确解希望也不大。所有这些都迫使人们去寻求能借助电子计算机来处理的新的数学模式。冯·诺依曼为此贡献了许多天才的方法:它们大多分载在各种实验报告中。从求解偏微分方程的数值近似解,到长期天气数值预报,以至最终达到控制气候等。
在冯·诺依曼生命的最后几年,他的思想仍甚活跃,他综合早年对逻辑研究的成果和关于计算机的工作,把眼界扩展到一般自动机理论。他以特有的胆识进击最为复杂的问题:怎样使用不可靠元件去设计可靠的自动机,以及建造自己能再生产的自动机。从中,他意识到计算机和人脑机制的某些类似,这方面的研究反映在西列曼讲演中;逝世后才有人以《计算机和人脑》的名字,出了单行本。尽管这是未完成的著作,但是他对人脑和计算机系统的精确分析和比较后所得到的一些定量成果,仍不失其重要的学术价值。
《经典力学的算子方法》
《量子力学的数学基础》(1932年)
來冯臫·頭筿诺依曼逝世后,未完成的手稿于1958年以《计算机与人脑》为名出版。他的主要著作收集在六卷《冯·诺依曼全集》中,1961年出版。
另外,冯·诺依曼40年代出版的著作《博弈论和经济行为》(与摩根斯顿合著),使他在经济学和决策科学领域竖起了一块丰碑。他被经济学家公认为博弈论之父。当时年轻的约翰·纳什在普林斯顿求学期间开始研究发展这一领域,并在1994年凭借对博弈论的突出贡献获得了诺贝尔经济学奖。
《程序内存》是诺伊曼的另一杰作。通过对ENIAC的考察,诺伊曼敏锐地抓住了它的最大弱点--没有真正的存储器。ENIAC只在20个暂存器,它的程序是外插型的,指令存储在计算机的其他电路中。这样,解题之前,必需先想好所需的全部指令,通过手工把相应的电路联通。这种准备工作要花几小时甚至几天时间,而计算本身只需几分钟。计算的高速与程序的手工存在着很大的矛盾。
针对这个问题,诺伊曼提出了程序内存的思想:把运算程序存在机器的存储器中,程序设计员只需要在存储器中寻找运算指令,机器就会自行计算,这样,就不必每个问题都重新编程,从而大大加快了运算进程。这一思想标志着自动运算的实现,标志着电子计算机的成熟,已成为电子计算机设计的基本原则。
1946年7,8月间,冯·诺依曼和戈尔德斯廷、勃克斯在ENIAC方案的基础上,为普林斯顿大学高级研究所研制IAS计算机时,又提出了一个更加完善的设计报告《电子计算机逻辑设计初探》.以上两份既有理论又有具体设计的文件,首次在全世界掀起了一股“计算机热”,它们的综合设计思想,便是著名的“冯·诺依曼机”,其中心就是有存储程序原则--指令和数据一起存储(存储机)。这个概念被誉为“计算机发展史上的一个里程碑”。它标志着电子计算机时代的真正开始,指导着以后的计算机设计。自然一切事物总是在发展着的,随着科学技术的进步,今天人们又认识到“冯·诺依曼机”的不足,它妨碍着计算机速度的进一步提高,而提出了“非冯·诺依曼机”的设想。
冯·诺依曼还积极参与了推广应用计算机的工作,对如何编制程序及搞数值计算都作出了杰出的贡献。冯·诺依曼于1937年获美国数学会的波策奖;1938年获得博谢纪念奖;1947年获美国总统的功勋奖章、美国海军优秀公民服务奖;1956年获美国总统的自由奖章和费米奖。

约翰·冯·诺依曼
2.据说有一天,冯·诺依曼心神不定地被同事拉上了牌桌。一边打牌,一边还在想他的课题,狼狈不堪地“输掉”了10元钱。这位同事也是数学家,突然心生一计,想要捉弄一下他的朋友,于是用赢得的5元钱,购买了一本冯·诺依曼撰写的《博弈论和经济行为》,并把剩下的5元贴在书的封面,以表明他“战胜”了“赌博经济理论家”,着实使冯·诺依曼“好没面子”。
3.在ENIAC计算机研制时期。有几个数学家聚在一起切磋数学难题,百思不得某题之解。有个人决定带着台式计算器回家继续演算。次日清晨,他眼圈黑黑,面带倦容走进办公室,颇为得意地对大家炫耀说:“我从昨天晚上一直算到今晨4点半,总算找到那难题的5种特殊解答。它们一个比一个更难咧!”说话间,冯·诺依曼推门进来,“什么题更难?”虽只听到后面半句话,但“更难”二字使他马上来了劲。有人把题目讲给他听,教授顿时把自己该办的事抛在爪哇国,兴致勃勃地提议道:“让我们一起算算这5种特殊的解答吧。”
大家都想见识一下教授的“神算”本领。只见冯·诺依曼眼望天花板,不言不语,迅速进到“入定”状态。约莫过了5分来钟,就说出了前4种解答,又在沉思着第5种……。青年数学家再也忍不住了,情不自禁脱口讲出答案。冯·诺依曼吃了一惊,但没有接话茬。又过了1分钟,他才说道:“你算得对!”
那位数学家怀着崇敬的心情离去,他不无揶揄地想:“还造什么计算机哟,教授的头脑不就是一台‘超高速计算机’吗?”然而,冯·诺依曼却呆在原地,陷入苦苦的思索,许久都不能自拔。有人轻声向他询问缘由,教授不安地回答说:“我在想,他究竟用的是什么方法,这么快就算出了答案。”听到此言,大家不禁哈哈大笑:“他用台式计算器算了整整一个夜晚!”冯·诺依曼一愣,也跟着开怀大笑起来。
4.冯诺依曼的驾驶水平很烂,经常发生事故,有一次他撞坏了车头,在警局里解释道:“我正在路上正常驾驶,右方窗外的树正在以60英里每小时的速度从我车旁穿过,突然,一棵树站在了我的车前,咚!”
5.在冯诺依曼临去世的前几天,肿瘤已经占据了他的大脑,但记忆力有时还是不可思议得好,那天乌拉姆坐在他的病榻前用希腊语朗诵一本修昔底德书中他特别喜欢的亚丁人进攻梅洛思的故事和佩里莱的演说,他记得很牢,会纠正乌拉姆的错误和发音。
认知能力
Hans Bethe(诺贝尔奖物理学获得者):I have sometimes wondered whether a brain like von Neumann's does not indicate a species superior to that of man. (我有时在思考冯诺伊曼这样的大脑是否暗示着存在比人类更高级的生物物种。)
David Blackwell:He was a really remarkable man.He listened to me talk about this rather obscure subject and in ten minutes he knew more about it than I did.He was extremely quick. (他是个出类拔萃的人,我给他大概地讲了一下我最近研究的课题,在十分钟之后他已经比我知道的更多了。他的思维真的是异常的敏捷。)
George Pólya:The only student of mine I was ever intimidated by. He was so quick.There was a seminar for advanced students in Zürich that I was teaching and von Neumann was in the class. I came to a certain theorem, and I said it is not proved and it may be difficult. Von Neumann didn't say anything but after five minutes he raised his hand. When I called on him he went to the blackboard and proceeded to write down the proof.After that I was afraid of von Neumann. (他是唯一的令我感到自己的教师地位受到威胁的学生,他实在是太敏锐了。有一次我在苏黎世为研究生们作演讲,当时冯诺依曼也在听课,我提出了一个悬而未决的问题,过了5分钟冯诺依曼举起了手,当我叫他的时候他径直走到了讲台前,写下了此问题的证明,自此之后我对冯诺依曼感到畏惧。)
Eugene Wigner(诺贝尔物理学奖获得者):他很有幽默感,因他这种讲故事和笑话的能力很受人即使是陌生人的喜爱,他可以在必要的时候变得简单快乐,但绝不轻浮愚蠢。冯诺依曼这种非凡的大脑需要理解大部分像我们一样的人不想去理解的甚至不奢求理解的东西。这个事实影响了冯诺依曼的道德判断,只有在科学上的错误和不和谐的地方会让他感到愤怒或者遗憾,在任何人犯了科学上面的错误时,他都会毫不犹豫地纠正别人的错误。
Herman Goldstine:他的一个非凡的能力就是绝对精准的记忆力,据我所知,冯诺依曼有能力看过一本书或者一篇文章后一字不错地背诵出来,更甚,他同样能够在多年以后不带丝毫犹豫地做到。他还可以将其实时翻译成英文背诵出来,而且速度丝毫不减。有一次我为了测试他的能力,问他《双城记》是怎么开头的,片刻,他开始背诵第一章节,直到可能10或者15分钟后我让他停下来。
成就评价

冯·诺依曼之墓
Glimm:he is regarded as one of the giants of modern mathematics. (他被普遍认为是现代数学的一位巨人。)
Jean Dieudonné:the last of the great mathematician. (最后一位杰出数学家。)
Peter Lax:20世纪最具科学头脑的人。
附件列表
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
